i finished reading Douglas Hofstadter's I Am a Strange Loop a few days ago. it was a really good book, and i'll probably have a lot more to say about it later, but one part in particular i really liked was the description of two incredible mathematical things: Euclid's Theorem on the infinitude of prime numbers, and Godel's Incompleteness Theorem on the impossibility of any rigid numeric system to be capable of describing every "true" thing. i will definitely talk about Godel's theorem in the future because it's so so so cool, but Euclid's theorem is a super succinct, pleasant little theorem that Hofstadter described as one of the most important achievements of humanity, whose proof is something everyone needs to experience (comparable to tasting chocolate and listening to music). here is my attempt to describe it and hopefully convey what makes it so wonderful.
The Infinite Set of Primes
to begin, a "prime number" is a number that is only divisible by 1 and itself. the first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. the number 100 is not a prime number because it is divisible by 1, 2, 4, 5, 10, 20, 25, 50, and 100, while the number 101 is a prime number because it is only divisible by 1 and 101.
so, how do we know that there are an infinite number of primes? first, notice how there is only a single prime number that is even (2, the very first prime number). half of all integers are even, so this automatically cuts out 50% of all numbers from being candidates of primality! and the odds are not looking good; the next prime number, 3, cuts out between 25-33% of all integers from being prime, too! this means when i pick any random number (e.g., 227472) it is pretty likely that this number will be divisible by either 2 or 3 (in this case, 227472 is divisible by 3, which makes it not prime; a number which is not prime is called composite). it's natural to look at this pattern and think "well if we keep getting more and more prime numbers, there's gotta be a point in which EVERY super big random number (say, 18593824123...3831) is divisible by SOME number before it, right? there's so many numbers in the world that there MUST be some point where every number after that point has at least one factor, right??"
now, the difficulty of answering this question using intuitive means is when you attempt an empirical method (e.g., "let me choose a super big random number like 18593824123...3831 and test to see if its prime") and find that it IS prime, you can't really use that to justify if there are an INFINITE amount of primes. what if the very last prime number is, i dont know, a little bit higher than the number you chose? how can you PROVE that its infinite? well luckily, some guy from 300 BC found out a cool way to prove this!
before i describe it, i want to first point out that our modern way of describing proofs (e.g., with nice looking formulas, "equals" signs (=), and the number zero (0), to say the least) did not exist until like a few hundred years ago. you had to describe things in prose. if i wanted to tell you the quadratic formula, i would have to say "there are three variables in a quadratic formula equaling the three coefficients corresponding to the first (squared), second (linear), and third (zeroed) products of an inputted variable. the result is a fraction: the numerator is the second coefficient plus or minus the square root of negative the squared term minus the product of four times the first term times the third term; the denominator is negative two times the first term." this sucks right. the greeks didnt really do algebra, they basically only did geometry since they thought thats all there really was to math, so they didnt necessarily need all the fancy tools that come with algebra (you can describe geometrical proofs in prose relatively easily).
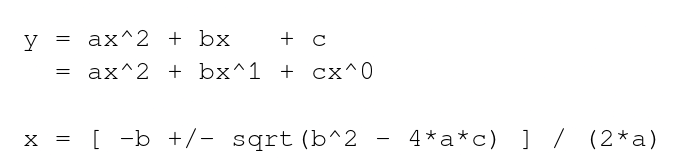
ok here's what you've been waiting for. make sure you're sitting down. it rocks. prepare yourself.
notice that all composite (non-prime) numbers can be decomposed into the products of only prime numbers. taking our previous example of 100, this can turn into 25 times 4; this is equivalent to saying 5 times 5 times 2 times 2; and each of these numbers (5 and 2) are prime themselves. you can do this for any composite number, no matter how large: they are each composed of products of prime numbers.
so let's assume that there IS actually a finite number of primes. this would mean that there is a "last" prime number, the "Great Final Prime". this may mean the Great Final Prime has, i dont know, a million billion digits in it, but lets assume it exists. now, let's create a set of ALL prime numbers between 2 and the Great Final Prime. since we have a "last" prime number, this will turn out to be a finite set of numbers. now here's the fun part: multiply each of these prime numbers together to create a brand new, monstrously large Mega Number.
before we go any further, here's a little quiz to see if you understand this post so far! is the Mega Number prime or composite? i asked this to my dad while i was explaining it to him and he got the wrong answer so think about it for a few seconds and then scroll down to the very end of this blog post to see the answer. :+)
ok, so we've just made this disgustingly large number. if the Great Final Prime number was a million billion digits, then the Mega Number's gotta be like, a million billion to the power of a million billion to the power of ... to the power of a million billion digits. its huge. (although dont fact check me on that part i dont actually know how large it is, the size of the Mega Number isn't important.)
but wait! hopefully you saw at the end of this post that the Mega Number is not prime! since it's got a bunch of factors, it's like, super composite. but we're not done yet! all we need to do is add one to the Mega Prime...
that's it! we've made a new prime number! "huh??", i hear you asking, "why is that?? can you PROVE it?!" well, yes! let's look at this simply: the Mega Number plus one (let's call it the Mega Prime) is NOT divisible by two, since the Mega Number itself WAS divisible by two (and an even number plus one would be an odd number, meaning the Mega Prime must be odd!). the next prime number is three: the Mega Prime is NOT divisible by three, since it is one higher than the Mega Number which WAS divisible by three (this is like saying "if 27 was the Mega Number, then 27 is divisible by 3, but 27 + 1 is not divisible by 3). the next prime number is five, which follows the same explanation as before. in fact, since we multiplied EVERY prime number (before the Great Final Prime) together to form this NEW Mega Prime, we can be ABSOLUTELY CONFIDENT that the Mega Prime IS in fact a prime number!
and there you have it! we've just proven that the Great Final Prime is actually NOT the "final prime number" since we have discovered at least ONE MORE prime number that is larger than it! though what about the nay-sayers who say "nay, what if that Mega Prime just becomes a brand NEW Great Final Prime (perhaps we can call it the Neo Great Final Prime)? we've just done a catch-22, creating a brand new problem!" but this is solved simply: just repeat the process! multiply all the discovered primes together (e.g., from 2 to the Neo Great Final Prime), add one to that number, and that's a new, even larger prime. we can repeat ad infinitum to keep generating new prime numbers, which proves the set of all primes is, in fact, infinite.
Waow!
Waow! how fun! i hope you like this little proof. please ruminate on it a little while, and recount it to all your friends the next time one of them says "math is for the dogs, this stuff sucks!" well maybe math IS for the dogs, but in a cool way! maybe the dogs LIKE the math and think its cool and fun!
if you liked this, i'll be posting more math stuff in the future. i've been avoiding making a blog post lately because i wanted to make sure my posts were Perfect and Polished and Everything, but this made me horribly unmotivated, as i talked about in my previous blog post (which i famously declared i would return to weekly posts. dont check how long ago i made that post). i found out im a perfectionist, but in a bad way. "perfectionism" sounds like one of those flaws you would put in a resume to make it seem like you're bragging instead of saying an actual flaw, but i think it describes a genuine thing i want to improve on and not worry so much about. i'll make some future post describing it more, maybe. one small thing im doing to avoid this is by not typing in capital letters; it's a tiny way to signal to myself that "im not going to work on making this post perfect."
ok, so next post will be about maybe some of the books im reading. i want to talk about quantum physics, too. i can also talk about the miller-rabin method of primality testing to keep on the subject of prime numbers. Godel's incompleteness theorem will also definitely come because it ROCKS but i want that post to be nicer. i WILL make another post within the next week. be on the lookout! in any case, if you wanna say hi, my discord is urlslug and my twitter is also URLSlug. :+)
-Sophie
question 1: is the Mega Number prime or composite?
Composite! the factors of the Mega Number would be:
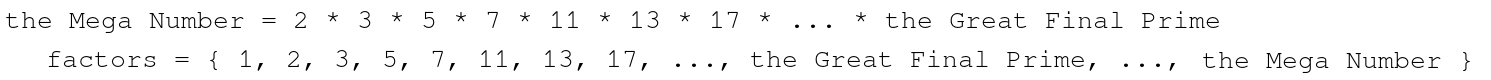
since the Mega Number has more factors than just 1 and itself, it is composite and not prime.